Предыстория
В отечественной статистической практике отношение к проверкам на нормальность и выбору между параметрическими и непараметрическими тестами проходило несколько витков. Сначала проверки на нормальность просто не делали и по умолчанию применяли t-тест. Потом многие стали внимательнее читать учебники и узнали про допущения теста Стьюдента, в частности, про нормальность распределения, и о том, что ее надо проверять (но почему-то речь шла о нормальности распределения данных, а не о распределении выборочных средних).
Классический пайплайн проверки включал тесты Шапиро-Уилка и/или Колмогорова-Смирнова: если тест Шапиро-Уилка отвергает нулевую гипотезу о нормальности, идем в непараметрику; если не отвергает — «значит нормально» и можно делать t-тест. Параллельно сложилась полуформальная блок-схема: тест на нормальность → в зависимости от результата делаем параметрический t-тест или непараметрический, например, Манна-Уитни. В какой-то момент это стало очень распространенной обязательной двухшаговой процедурой.
Классический пайплайн проверки включал тесты Шапиро-Уилка и/или Колмогорова-Смирнова: если тест Шапиро-Уилка отвергает нулевую гипотезу о нормальности, идем в непараметрику; если не отвергает — «значит нормально» и можно делать t-тест. Параллельно сложилась полуформальная блок-схема: тест на нормальность → в зависимости от результата делаем параметрический t-тест или непараметрический, например, Манна-Уитни. В какой-то момент это стало очень распространенной обязательной двухшаговой процедурой.
Дальше практика применения тестов и проверок на нормальность снова изменилась. Обсуждения в профессиональных чатах и еще более внимательное чтение учебников постепенно привели к выводу: требование нормальности касается не исходных данных как таковых, а распределения выборочных средних. При достаточно больших выборках это гарантируется центральной предельной теоремой (ЦПТ) — в случае генеральных совокупностей с конечной дисперсией.
Распределения же с бесконечной дисперсией, например, распределение Коши, не встречаются на практике.
Из-за этого и возникают многочисленные ошибки интерпретации: многие проверяют нормальность исходных данных (выборки) и делают на основе этого выводы о применимости t-теста, хотя корректнее думать о распределении средних. Впрочем, при нормальном распределении выборки нормальность распределения выборочных средних гарантируется.
Выборочные средние
Что такое выборочные средние проще показать на интерактивной иллюстрации ЦПТ (Shiny App): берём генеральную совокупность, выбираем из нее множество выборок фиксированного объема, для каждой считаем среднее и строим гистограмму этих средних. Если исходное распределение нормальное, выборочные средние тоже распределены нормально.
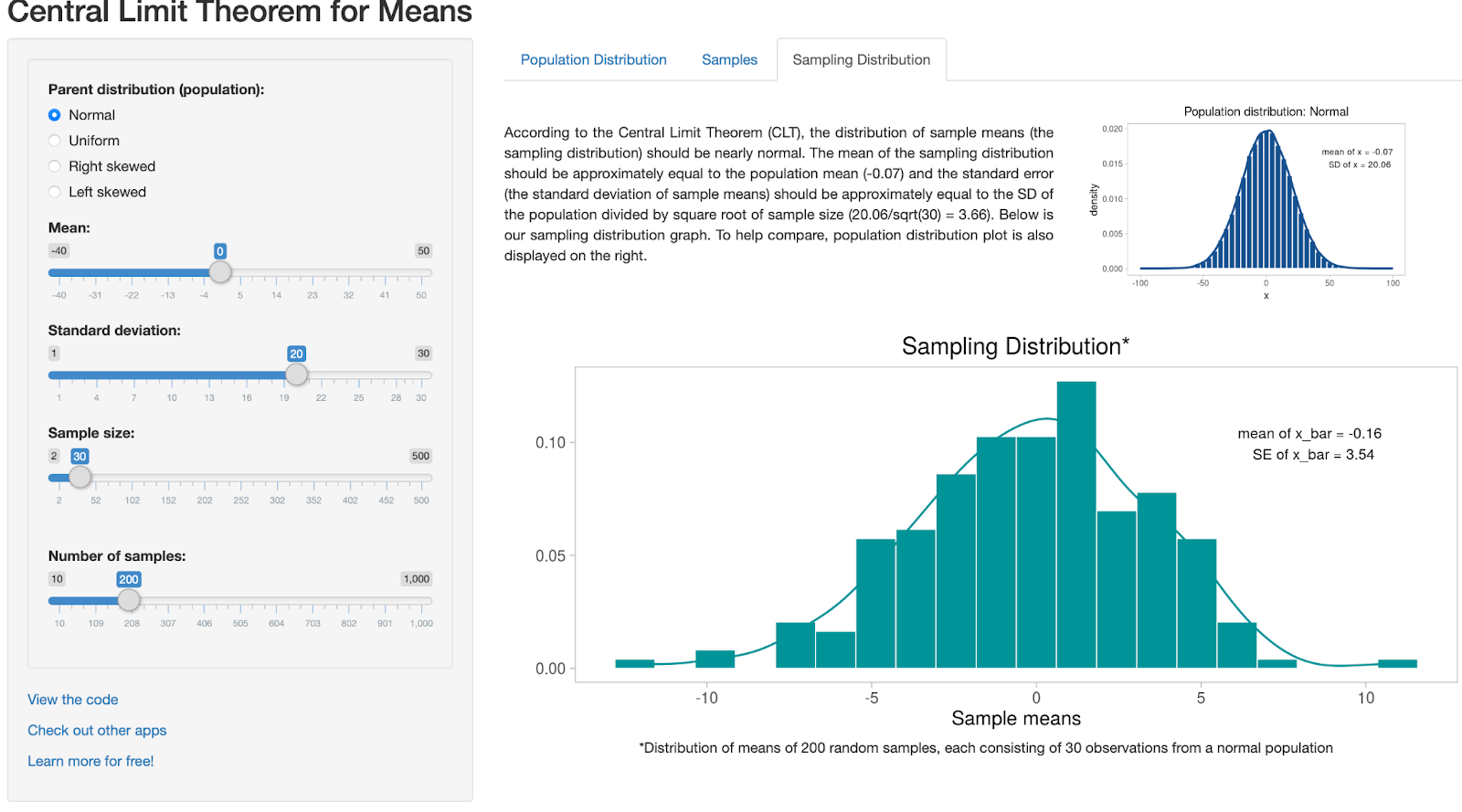
Но магия ЦПТ в том, что и при ненормальных исходных распределениях (например, равномерном или выраженно скошенном) при достаточно большом n распределение выборочных средних всё равно близко к нормальному. Если же размер выборки n уменьшать, нормальность выборочных средних ухудшается — особенно при сильной асимметрии и «тяжёлых хвостах».
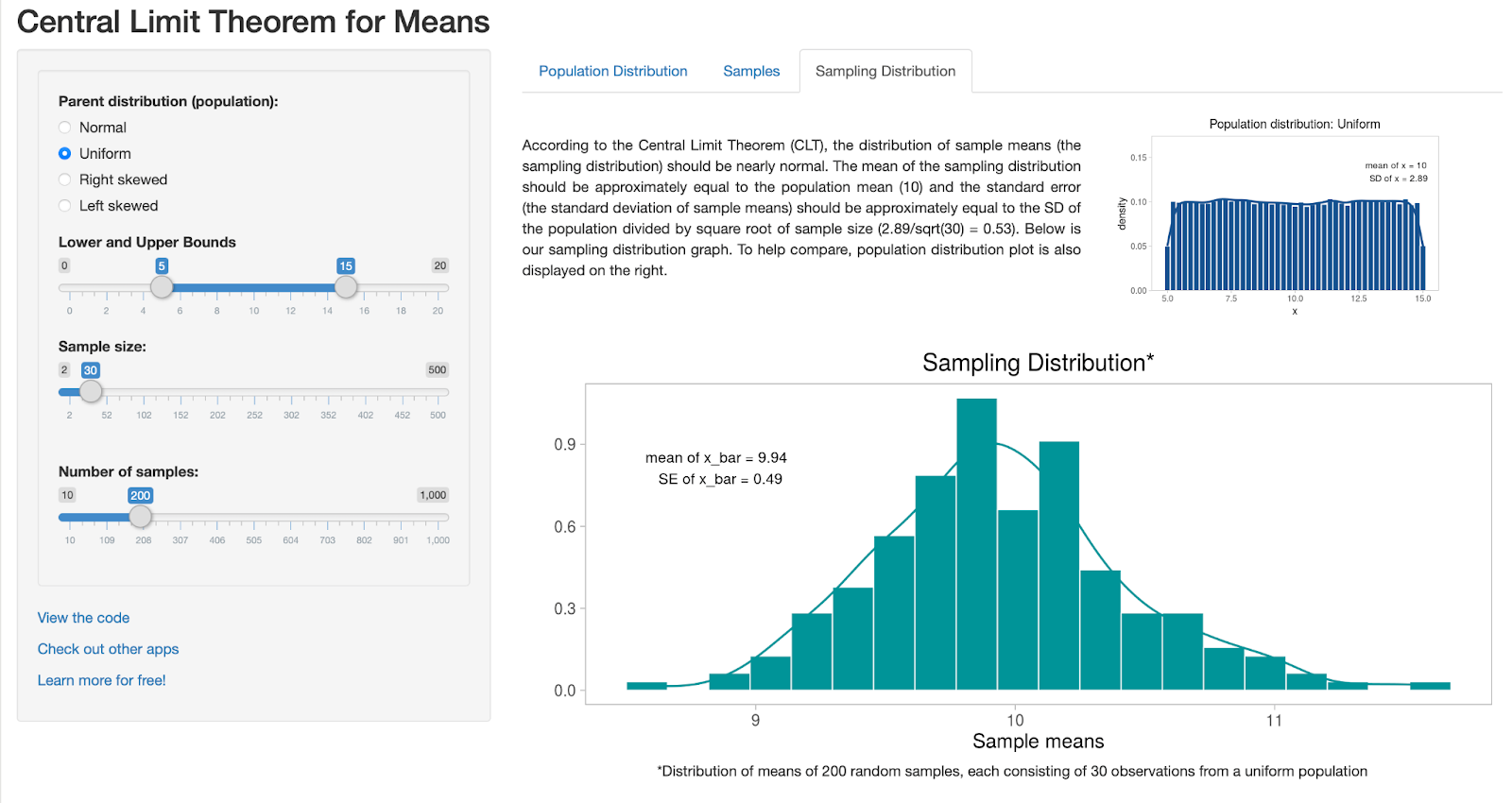
Таким образом, даже для генеральной совокупности, распределение которой отличается от нормального, при достаточно большой выборке, выборочные средние будут распределены нормально в силу ЦПТ.
Что такое достаточно большая выборка — это тема для отдельной дискуссии.
Любопытный факт
Если же генеральная совокупность распределена нормально, то даже при малых выборках, распределение выборочных средних будет нормальным. Это можно проверить с помощью симуляции:
#код на R
pop <- rnorm(100000)
hist(replicate(1000, mean(sample(pop, 2))))Здесь исходная генеральная совокупность pop со средним 0 и стандартным отклонением 1. Далее мы 1000 раз извлекаем выборки размером 2 и строим гистограмму выборочных средних, которые оказываются распределены нормальным образом. Но, к сожалению, мы почти никогда не знаем, распределена ли наша генеральная совокупность нормально.
Проверки на нормальность и гомогенность дисперсий
Для проверки соответствия данных нормальному распределению есть ряд тестов, наиболее распространенные — тест Шапиро-Уилка и Колмогорова-Смирнова. Более подробно разберем на примере теста Шапиро-Уилка. Нулевая гипотеза теста в том, что выборка происходит из нормального распределения. Если p-value в тесте < 0.05 — то мы отвергаем нулевую гипотезу. Если p-value > 0.05 — это еще не значит, что выборка обязательно происходит из нормального распределения, а означает лишь то, что мы не смогли отклонить нулевую гипотезу. То есть для теста характерна та же асимметричность, как и для любого другого статистического теста. Отсюда первая проблема: на больших выборках тест имеет высокую мощность и находит микроскопические отклонения, которые для применения t-теста несущественны (ЦПТ страхует). На малых выборках у теста мало мощности, и он может «не заметить» существенную ненормальность как раз там, где ЦПТ еще не помогает. Поэтому двухступенчатая схема из дорожных карт по статистике (сначала Шапиро-Уилк, затем выбор теста) мало полезна.
Но это еще не всё. Основная проблема двухступенчатой схемы — это замена нулевой гипотезы, в зависимости от результата теста Шапиро-Уилка. Когда мы планируем эксперимент, у нас есть определенное понимание исследовательского вопроса и контекста, например, если мы хотим сравнить средние чеки, то нулевая гипотеза должна формулироваться именно про равенство средних. Мы не можем корректно заменять одну гипотезу другой только из-за исхода вспомогательного теста на нормальность.
Важно понимать: тест Манна-Уитни совсем не «непараметрическая замена» тесту Стьюдента, это другой тест со своей нулевой гипотезой и своими ограничениями. Нулевая гипотеза в тесте Манна-Уитни — это так называемый сдвиг распределений (location shift), то есть то, насколько одно распределение сдвинуто относительно другого. В частных случаях это действительно может означать проверку равенства медиан (отсюда и происходит распространенный миф), но в общем случае тест Манна-Уитни не обязан интерпретироваться именно так.
Про тест Велча
В дорожных картах статистики есть и про проверку гомогенности дисперсий, где могут советовать применять тест Стьюдента, если дисперсии равны, и тест Велча, если дисперсии не равны. Здесь та же самая проблема, что и в двухступенчатой схеме с проверкой на нормальность тестом Шапиро-Уилка. Однако здесь проще дать рекомендацию: можно применять тест Велча по умолчанию, в большинстве случаев он будет практически неотличим от теста Стьюдента, но при большом дисбалансе дисперсий и размера выборки, тест Велча лучше контролирует ошибку первого рода (на заданном уровне альфа, например 0.05). Ссылка на более подробный разбор, а возможное возражение — тут.
Применимость t-теста
Где вообще уместен t-тест? В общем случае — когда у нас гипотеза о среднем. Например, мы хотим сравнить высоту растений двух видов и для этого измерили несколько десятков образцов растений в сантиметрах. И наша нулевая гипотеза касается равенства средних, здесь t-тест уместен при соблюдении остальных допущений (в частности, нужно не забывать о требовании независимости данных).
Но для ранговых данных (например, оценка тяжести заболевания, обычно от 1 до 4 или классический опросник Ликерта с оценкой по шкале от 1 до 7 вида «полностью не согласен … полностью согласен») не выполняется предположение о равенстве интервалов между делениями шкалы (от 1 до 2 может быть больше информации, чем от 3 до 4), и среднее — теоретически не определено. В этом случае мы не сравниваем средние, а можем сравнивать распределения, поэтому более обоснованно использовать непараметрические тесты (Манна-Уитни/Вилкоксона/Краскела-Уоллиса — в зависимости от количества групп и дизайна эксперимента).
Однако, это сложный вопрос с точки зрения психометрики: шкала Ликерта может считаться квазинепрерывной, и тогда для нее становятся применимы гипотезы о средних. Один (но не единственный) из используемых подходов здесь — обращать внимание на число делений шкалы. Для суммарных опросных шкал с большим числом категорий (например, сумма по множеству пунктов, диапазон от 0 до 100) возможен квази-интервальный подход: при большом числе «делений» неравенство интервалов сглаживается, и многие исследователи осторожно используют параметрические методы. Это не строгая математика, а практическая конвенция психометрики. Если уверенности в примерном равенстве интервалов между делениями шкалы нет — лучше оставаться в ранговых методах.
То есть при наличии четкого обоснования у исследователя можно относиться к порядковой шкале как к интервальной.
Другие ограничения t-теста
Более важный критерий — это независимость данных, про что иногда забывают.
Кроме этого, надо подчеркнуть, что для корректности t-теста важна не только нормальность выборочного среднего, но и распределение выборочной дисперсии. Именно это утверждает лемма Фишера: если данные исходят из нормального распределения, то выборочная дисперсия (с учетом числа степеней свободы) подчиняется распределению χ². Таким образом, знаменатель в формуле t-статистики имеет χ²-распределение, а числитель (среднее) — нормальное. В комбинации это и дает t-распределение Стьюдента.
Преобразование данных
Частый вопрос: «А может привести данные к нормальности преобразованием (например, Бокс-Кокс) и сделать t-тест?» Преобразования могут быть уместны, например, логарифмирование для данных с экспоненциальной природой.
Многие биологические процессы имеют экспоненциальную природу, как деление клетки или удвоение ДНК в процессе ПЦР.
Но проблема в том, что мы теряем интерпретируемость, так как тестируем уже не исходную метрику, а логарифм/квадратный корень и т.п., и результаты труднее объяснять. Поэтому «приводить к нормальности любой ценой» — не универсальная стратегия; сначала хорошо бы понять, осмысленно ли преобразование для вашей метрики и дизайна.
Итоговые тезисы
- При достаточно больших n нормальность выборочных средних обеспечивает ЦПТ — параметрические тесты обычно уместны, но важна еще нулевая гипотеза о средних;
- Формальные тесты на нормальность на большом n излишне чувствительны, на малом — слабы; не стоит механически завязывать выбор теста на Шапиро–Уилк;
- При гетерогенных дисперсиях и несбалансированных выборках используйте Вэлча;
- Для ранговых/опросных данных — непараметрика или аккуратная квази-интервальная интерпретация;
- Преобразования применяйте только если они содержательно оправданы;
- Непараметрические тесты имеют собственные допущения — проверяйте их.
Источники и ссылки
- Лекция Матвея Славенко из цикла «Разрушители мифов» Института биоинформатики
- Телеграм-канал Елены по статистике и анализу данных: @stats_for_science
- Лонгрид о поправках на множественное тестирование: https://ubogoeva.github.io/R4Analytics/posts/multiple_testing.html
- Пост про MDE и расчет размера выборки: https://t.me/stats_for_science/111
- Пара ссылок про то, что делать с пропущенными значениями: раз и два



